在 運動控制 的場合,選擇適合的 坐標系 是很重要的.不同的機械結構或應用,適合的坐標系也不同.本文針對常見的 直線 與 分度座標,加以說明其特性與適用場合.一般而言,機械根據末端形式可區分為二類:(1)有限行程,(2)無限行程,代表性的例子分別如下:
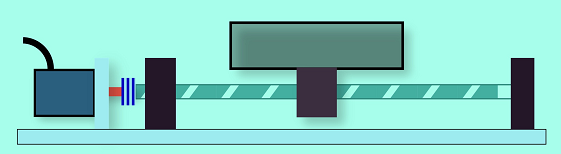
1,螺桿機構:二端有死點,行程有限,無週期性
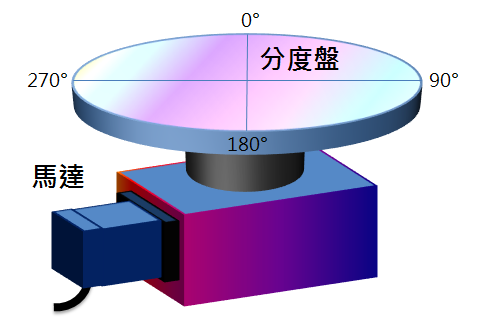
2,分度盤機構:沒有死點,行程無限,有週期性
週期性是指,馬達即使只往單方向旋轉,機構也會回到原來的位置,有周而復始的特性.現在的問題是:我們用伺服馬達來推動機構,可以知道馬達的位置(PLS),但真正關心的是機構(末端)的位置,馬達轉到哪裡其實不重要!那麼,該如何得到機構末端的位置呢?
直線坐標 位置計算:
以螺桿機構而言,機械的位置 與 馬達旋轉的脈波數 是 線性關係的:
機械位置 L(PUU)= 馬達脈波數(PLS)× 單位轉換 ...(1)[註 1]
這個 ” 單位轉換” 其實就是 電子齒輪比,L 表示機械末端的位置(PUU),與 馬達的脈波(PLS)是線性關係,所以 L 建立的坐標系就稱為 直線座標系,適合用來描述 直線運動機構 的位置!
分度坐標 位置計算:
然而,直線座標 適合 螺桿機構 卻不適合 分度盤,因為分度盤的位置永遠在360度的範圍內,不會隨馬達旋轉 無窮的變大.假設馬達轉4圈,分度盤剛好轉1圈,且馬達1圈對應的L=10000 PUU,若 馬達轉了 4,8,12 圈,則 分度盤分別轉 1,2,3 周,最終 角度 都一樣,但對應的 L=40000,80000,120000,… 卻不一樣!所以,用L來表示分度盤的位置並不適合,因為我們通常只在意最後的角度 而不是分度盤轉了幾週!所以必須定義一個新的坐標系來表示分度盤的位置,就是 分度座標,定義如下:
分度坐標 C(PUU)= MOD(L/L0)...(2)[註 2]
MOD:取得 除法的餘數.
L0 :分度坐標周長(PUU),即 分度一周 對應的L數量!
同上面的例子:分度盤轉1圈,馬達轉4圈,所以L0 =40000,假設馬達轉了 123 圈,分度盤的角度在哪裡呢?此時 L=1230000,很難看得明白,然而(2)式得到的分度坐標 C=30000,等於 3/4 周(L0 =40000),就能清楚知道目前在 270° 的位置了!因此 這類 旋轉機構 的位置用 分度座標 來描述要比 線性座標 清楚多了,使用上也更直覺!整理結論如下:
- 機構 有限行程:無週期性,有極限,適用 直線座標
- 機構 無限行程:有週期性,無極限,適用 分度座標
有了 分度坐標,運動控制器 就可以提供 分度定位 的命令,在 分度工作站,刀庫,刀塔,電子凸輪,都有很多的應用機會!
[註 1] 此為不考慮全閉環的情況,否則須將式中 馬達脈波數 更改為 光學尺 或 輔助編碼器 的脈波.
[註 2] 此式是數學上的表示法,實際計算時,因機構是無限行程,位置 L 會發生溢位,處理方法略為複雜!所以 分度坐標 不該由使用者來計算,而是由系統自動計算,才是功能完整的 運動控制器!